Independent and Dependent Events

From the multiplicative rule of probability, this can equivalently be expressed as:

which gives an intuitive notion of what independence means, being that the probability of $A$ is unchanged even it is known that $B$ occurred.

The notion of independence and dependence is a key distinguishing factor between working with probabilities and measure theory in general.

Viewing the probabilities as areas within the overall probability space, the notion of independence means that the proportion of the whole space taken up by $A$ is the same as the proportion of $B$ taken up by $A$. Here is an example:

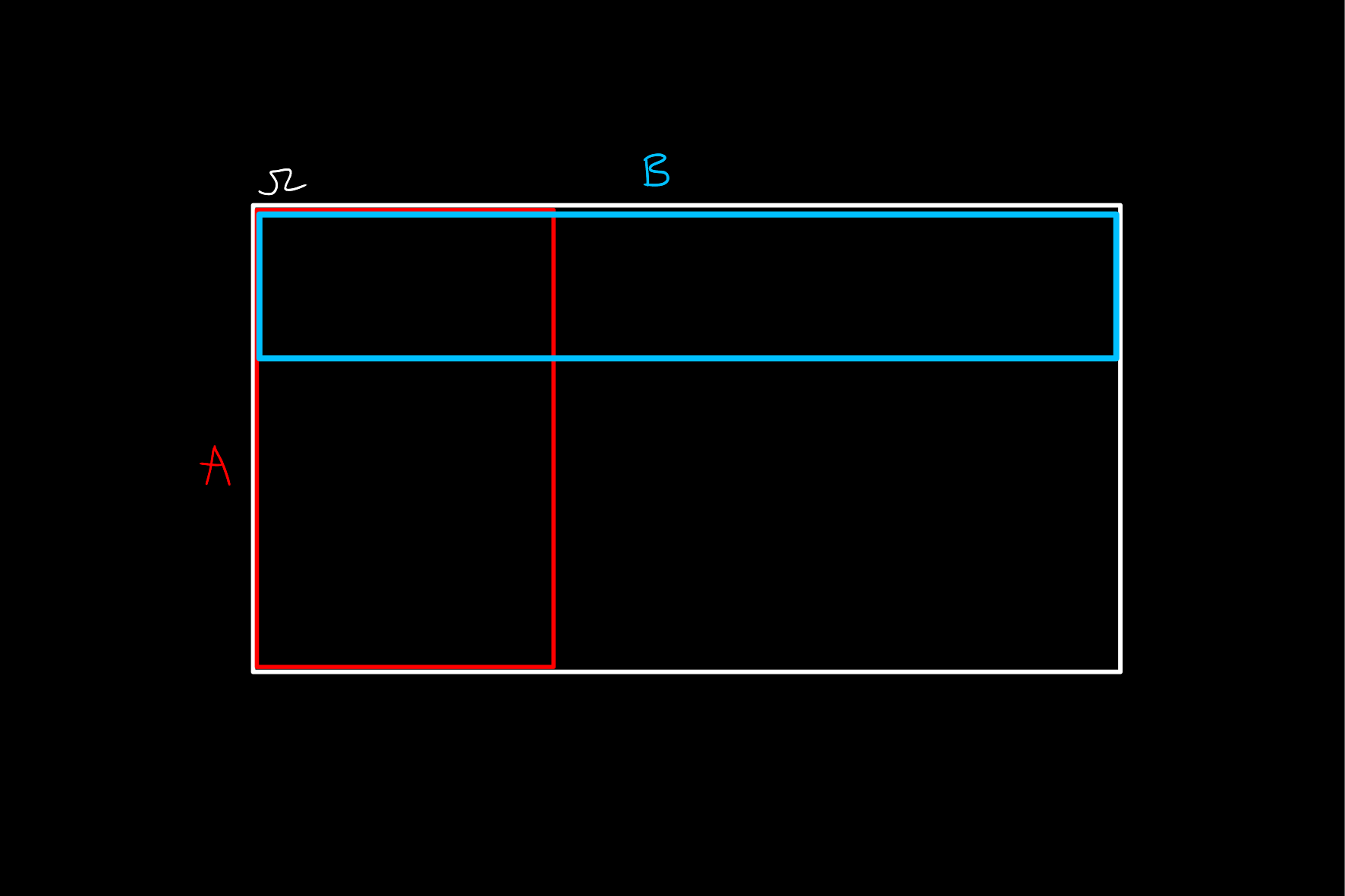
where $A$ takes up $\frac{1}{3}$ of the whole space,

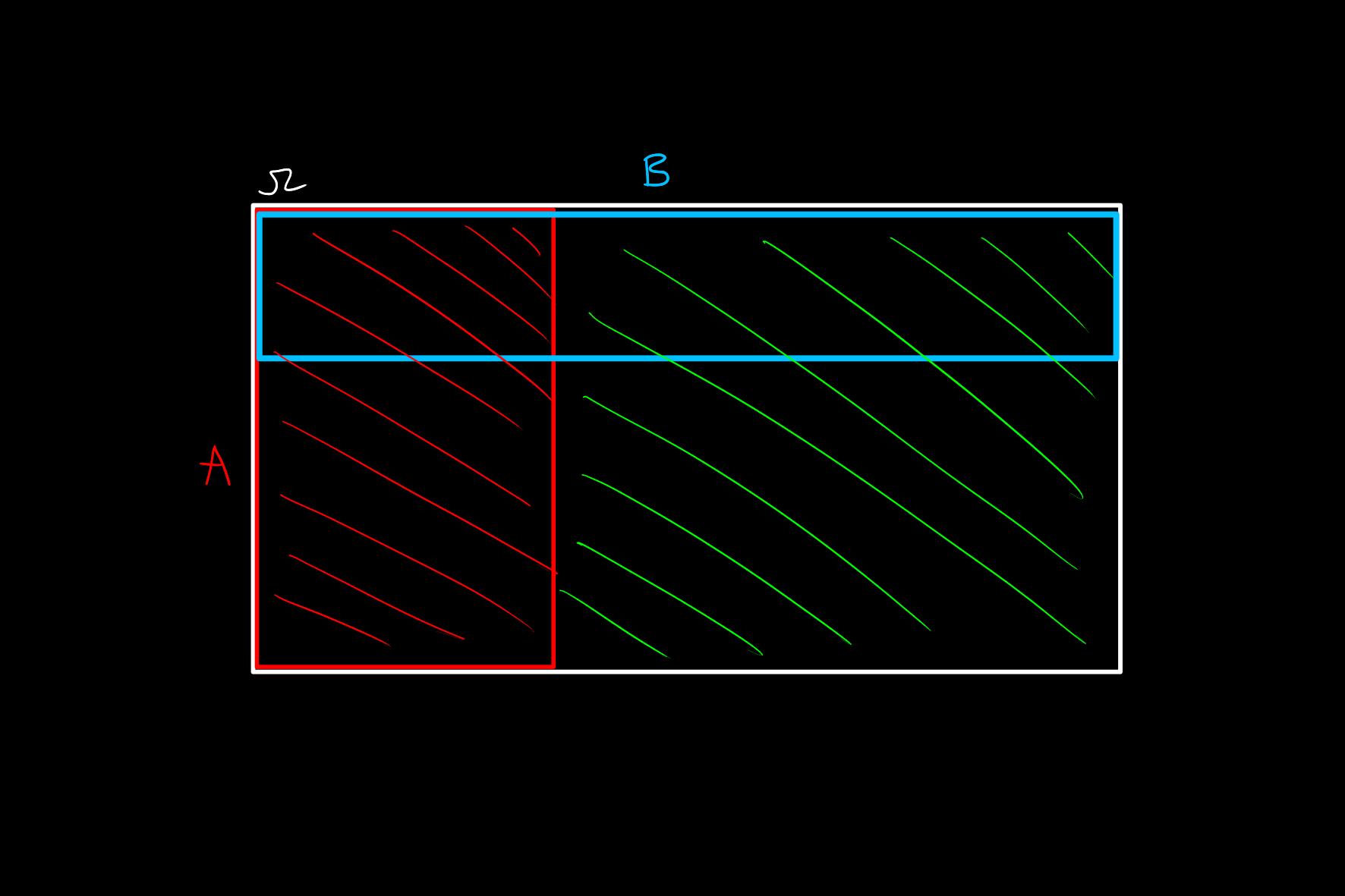
but the portion of it overlapping with $B$ also takes up $\frac{1}{3}$ of $B$:

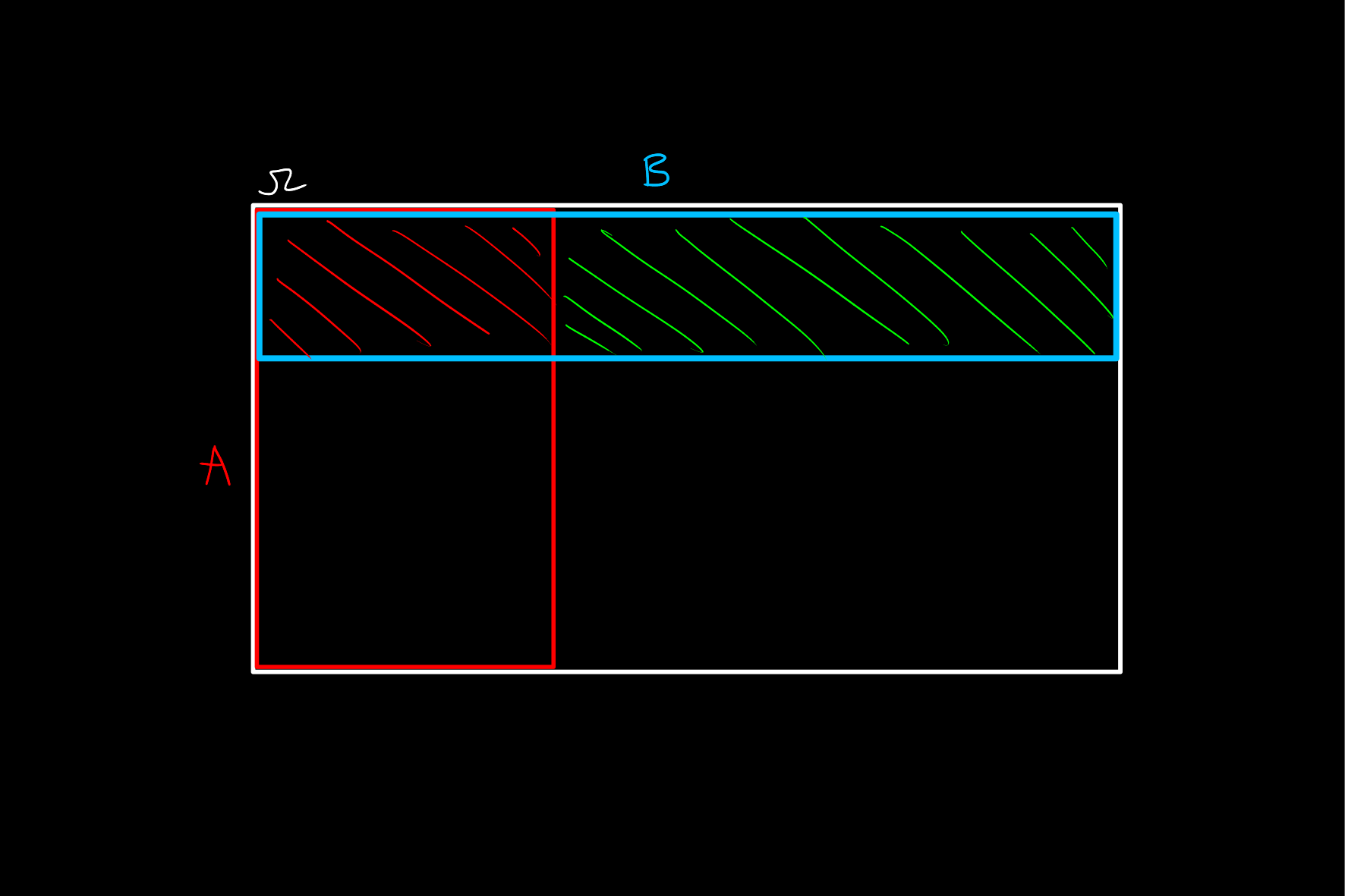
Drawing these probabilities as full width rectangles on perpendicular sides of the rectangle always yields independent events.